Angles Interior Are Consecutive Supplementary

The Properties Of Trapezoids And Isosceles Dummies

To help you remember: the angle pairs are consecutive (they follow each other), and they are on the interior of the two crossed lines.. parallel lines. when the two lines being crossed are parallel lines the consecutive interior angles add up to 180. (click on "consecutive interior angles" to have them highlighted for you. ). The theorem. the consecutive interior angles theorem states that the two interior angles formed by a transversal line intersecting two parallel lines are supplementary (i. e: they sum up to 180). If two angles are supplementary to two other congruent angles, then theyre congruent. (this is the four-angle version. ) the previous four theorems about complementary and supplementary angles come in pairs: one of the theorems involves three segments or angles, and the other, which is based on the same idea, involves four segments or angles.

Starting with the fact that angles 1 and a are a linear pair and that angles b and 2 are also a linear pair, use a two column proof to prove that consecutive interior angles a and b are supplementary. (5 points) statement reason a and b are supplementary. angle a is 145 deg and b is 35 deg, they equal 180. And because the bases are parallel, we know that if a transversal cuts two parallel lines, then the consecutive interior angles are supplementary. this means that the lower base angles are supplementary to upper base angles. midsegment of a trapezoid. The consecutive interior angles theorem states that if two parallel lines are cut by a transversal, then consecutive interior angles are supplementary (= 180) what is the alternate interior angles theorem? the consecutive interior angles theorem states that if two parallel lines are cut by a transversal, then each pair of alternate interior. Consecutiveinterioranglesconverse theorem. this page explains the consecutive interior angles converse theorem. use this section to learn this theorem in a simple way. this theorem states that if two lines are cut by a transversal so that the consecutive interior angles are supplementary, then the lines are said to be parallel.

Trapezoid Properties Visually Explained W 7 Examples

Are called consecutive interior angles. d and f are consecutive interior angles. c and e are consecutive interior angles. when the two lines are parallel, any pair of consecutive interior angles add to 180 degrees. play with it below (try dragging the points):. Perhaps the hardest property to spot in both diagrams is the one about supplementary angles. because of the parallel angles interior are consecutive supplementary sides, consecutive angles are same-side interior angles and are thus supplementary. (all the special quadrilaterals except the kite, by the way, contain consecutive supplementary angles. ) heres an isosceles trapezoid proof for. Find the value of x given that (3x + 20) and 2x are consecutive interior angles. solution. consecutive interior angles are supplementary, therefore; (3x + 20) + 2x = 180 3x + 20 + 2x = 180 5x + 20 = 180. subtract 20 from both sides 5x = 160. divide each side by 8. x = 32. hence, the value of x is 32 degrees. the.

Types Of Angles Vertical Corresponding Alternate Interior

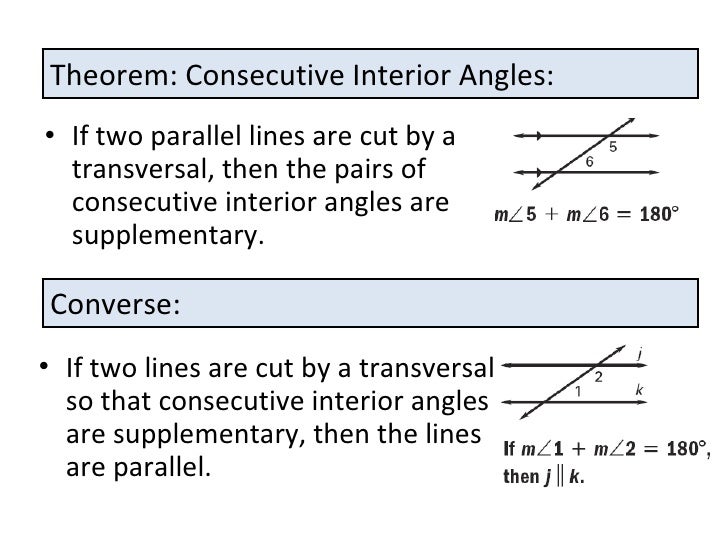
Alternate interior angles are the pair of non-adjacent interior angles that lie on the opposite sides of the transversal. in the above figure, the pairs of alternate interior angles are: 1 and 3 ; 2 and 4; co-interior angles. co-interior angles are the pair of non-adjacent interior angles that lie on the same side of the transversal. Consecutive interior angles are the two pairs of angles that: have distinct vertex points, lie on the same side of the transversal and; are both interior. two lines are parallel if and only if the two angles of any pair of consecutive interior angles of any transversal are supplementary (sum to 180). Learn about alternate interior angles: when two lines are crossed by another line (called the transversal), alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. Formally consecutive interior angles may be defined as two interior angles lying on the same side of the transversal cutting across two parallel lines. since the figure is a parallelogram. the angles bcd and dcf are adjacent supplementary angles and make in sum the straight angle bcf of 180.

So are angles 3 and 5. consecutive interior angles are supplementary. formally, consecutive interior angles may be defined as two interior angles lying on the same side of the transversal cutting across two parallel lines.

Updated Learning Consecutive Angles Are Supplementary

The properties of trapezoids and isosceles dummies.

Looking At The Consecutive Interior Angles 9 Points Look

The same-side interior angle theorem states that when two lines that are parallel are intersected by a transversal line, angles interior are consecutive supplementary the same-side interior angles that are formed are supplementary, or add up. himplasia/]effective 30caps himplasia[/url] vaadi herbals products supplementary approaches there are other approaches to franchise the sharing of appreciation

When parallel lines get crossed by a transversal many angles are the same, as in this example: see parallel lines and pairs of angles to learn more. vertically opposite angles corresponding angles alternate interior angles alternate exterior angles consecutive interior angles geometry index. In the diagram above, angles 2 and 3 are consecutive interior angles, and angles interior are consecutive supplementary so are angles 6 and 7. with the exception of vertical angles, all of these relationships can only be formed when two lines. Mathispower4u. wordpress. com/. Those two angles are consecutive. so are all these pairs: e and a a and r r and b; consecutive angles have endpoints of the same side of the polygon. supplementary angles. supplementary angles are two angles adding to 180. in a parallelogram, any two consecutive angles are supplementary, no matter which pair you pick.

In the figure, the angles 3 and 5 are consecutive interior angles. also the angles 4 and 6 are consecutive interior angles. consecutive interior angles theorem if two parallel lines are cut by a transversal, then the pairs of consecutive interior angles formed are supplementary. proof: given: k l t is a transversal. In the figure, the angles 3 and 5 are consecutive interior angles. also the angles 4 and 6 are consecutive interior angles. consecutive interior angles theorem if two parallel lines are cut by a transversal, then the pairs of consecutive interior angles formed are supplementary. proof: given: k l t is a transversal. 4 sides. sum of interior angles = 360 kite diagonals are perpendicular. 1 diagonal is a line of symmetry. parallelogram opposite sides are congruent. opposite angles are congruent. consecutive angles are supplementary. diagonals bisect each other. +5 more terms.

Consecutiveinteriorangles are the two pairs of angles that: have distinct vertex points, lie on the same side of the transversal and; are both interior. two lines are parallel if and only if the two angles of any pair of consecutive interior angles of any transversal are supplementary (sum to 180). Strategy. the definition of a parallelogram is that both pairs of opposing sides are parallel. therefore, its a simple use of the properties of parallel lines to show that the consecutive angles are supplementary.. we have already proven that for the general case of parallel lines, a transversal line creates interior angels that sum up to 180.. but, a parallelogram is simply two pairs of. Therefore, two consecutive angles abc and bcd are non-adjacent supplementary angles and make in sum the straight angle of 180. so, the theorem 1 is proved for the consecutive angles abc and bcd too. for the rest of consecutive angles the proof is similar. thus the theorem 1 is fully proved.

The 2 angles in purple (d and e) make one pair of consecutive interior angles, and the other 2 angles in red (c and f) make another pair of consecutive interior angles. both pairs are between the 2 lines and are both on the same side of the transversal. transversal is the line crossing the other two lines. identifying consecutive interior angles. Note: consecutive interior angles are supplementary angles, i. e. they add up to 180\(^\circ\). this can be proved by the consecutive interior angles theorem which states that "if a transversal intersects two parallel lines, each pair of consecutive interior angles are supplementary (their sum is 180\(^\circ\. ". The consecutive interior angles theorem states that when the two lines are parallel, then the consecutive interior angles are supplementary to each other. supplementary means that the two angles.